(자료구조 - 6) 트리(Tree)

트리 자료구조 소개, 이진 탐색 트리 설명

게시 2024/02/01

10 분읽는 시간

1) Tree 소개

트리(Tree) 자료 구조에 대해 알아보자.

트리는 노드(node)와 브랜치(branch, edge)를 사용해서 사이클이 이루어지지 않도록 구성된 자료 구조이다. 여기서 사이클이 이루어지지 않는다는 의미는 한 노드에서 시작해서 다른 노드들을 순회하여 자기 자신에게 돌아올 수 있는 순환이 없다(Acylic)는 뜻이다. 트리 자료 구조는 그래프의 일종이다.

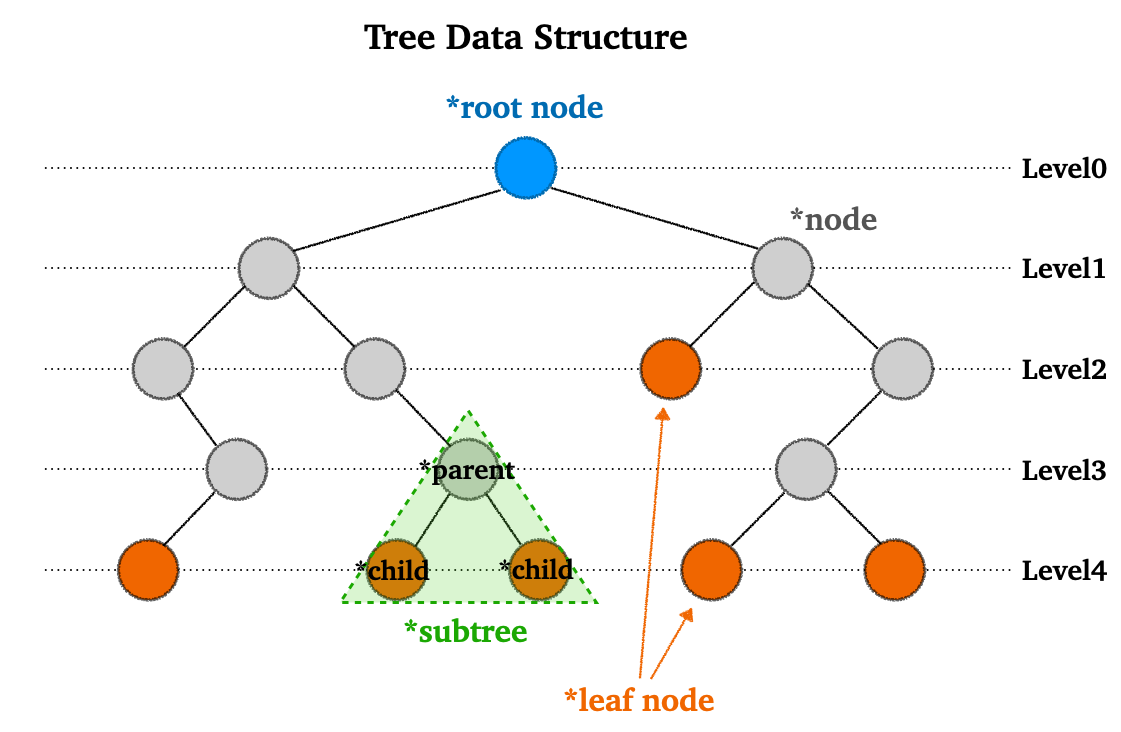
트리 구조를 다음 그림으로 이해해보자.

Tree Data Structure

노드(node) : 데이터를 저장하는 기본 요소
루트 노트(root node) : 트리의 가장 최상위 노드
단말 노드(leaf node) : 자식이 없는 노드
보조 트리(subtree) : 전체 트리에 속하는 일부 트리. 트리의 하위 집합으로 표현하기도 한다.
각 레벨(level)은 트리의 깊이를 나타낸다

트리 구조에 대한 설명을 더 하자면, 자식이 2개 까지 올 수 있는 트리를 이진 트리(binary tree)라고 한다. 자식 n개 까지 오면 n진 트리가 되지만, 보통 이진 트리를 가장 많이 사용한다. 이런 트리 구조는 많은 경우 탐색(검색), 정렬 알고리즘의 구현이나 위해서 사용된다. (그렇다고 탐색과 정렬만 할 수 있다는 뜻은 아니다!)

대표적인 이진 트리의 종류에는 다음이 있다.

이진 탐색 트리(BST, Binary Search Tree)
균형 이진 탐색 트리(Balanced Binary Search Tree)
- AVL 트리
- Red-Black 트리 : 자바 컬렉션의 TreeSet이 사용한다
B-Tree : 데이터베이스 인덱싱에 사용
Heap : 우선순위 큐를 구현하기 위해 사용 가능

2) 이진 탐색 트리(BST)

2.1 이진 탐색 트리 입력

이진 탐색 트리(BST)의 원리를 자세히 알아보기 전에 간단하게 설명하자면 부모 노드의 왼쪽 자식 노드에 더 작은 값을 넣고, 오른쪽 자식 노드에 더 큰 값을 넣는 방식으로 진행된다.

이제 부터 자세한 원리를 알아보자.

위에서도 설명했듯이 트리는 기본적으로 노드로 이루어져있다.

  


class Node {
  Object item;
  Node left;
  Node right;
}

각 노드는 왼쪽, 오른쪽 노드를 알고 있다
자바의 LinkedList 구현 처럼 각 노드의 참조를 통해 연결되어 있다

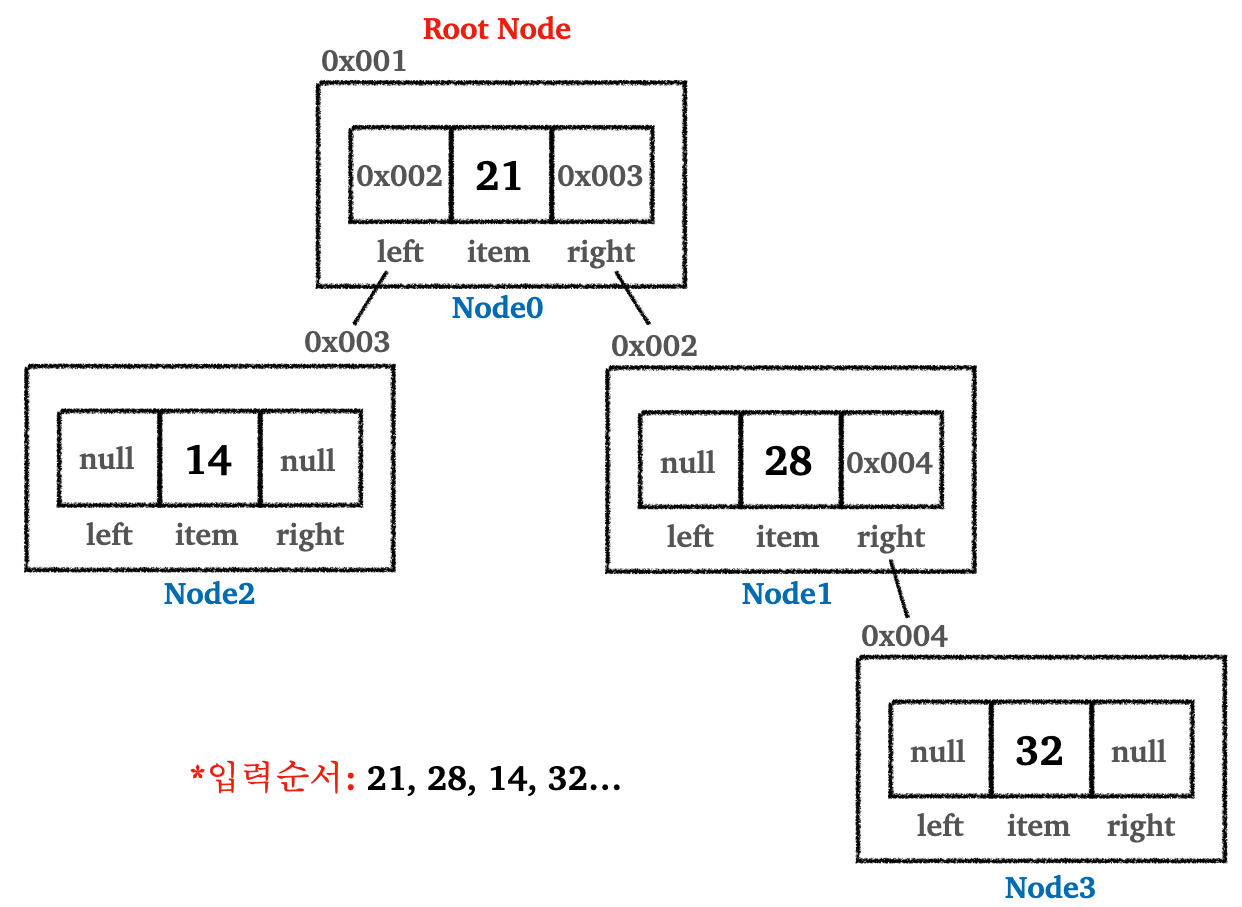
이진 탐색 트리의 핵심은 데이터 입력 시점에 정렬해서 보관한다는 점이다. 이때 데이터의 입력은 루트 노드 부터 시작해서, 부모 노드의 기준으로 작으면 왼쪽 자식 노드에 보관하고, 크면 오른쪽 자식 노드에 보관하면 된다.

데이터를 21, 28, 14, 32 ... 으로 계속 입력한다고 가정해보자.

루트 노드 21에 비해 28이 크기 때문에 28을 오른쪽 자식 노드에 보관
14는 위에서 부터 시작해서 21 보다 작기 때문에 왼쪽 자식 노드에 보관
32 > 21 : 오른쪽 서브 트리로 이동, 레벨 1 증가 → 32 > 28 : 오른쪽 자식 노드에 보관

글로 이해하기 어려울 수 있기 때문에 다음 애니메이션으로 데이터가 입력되는 과정을 살펴보자.

https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php

2.2 이진 탐색 트리 검색

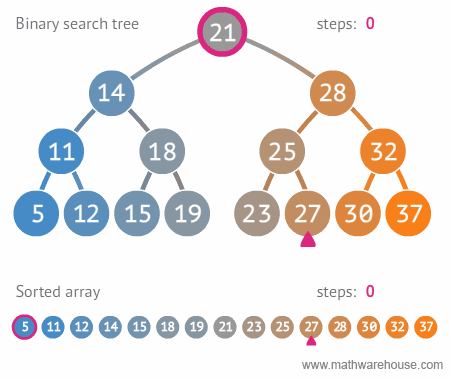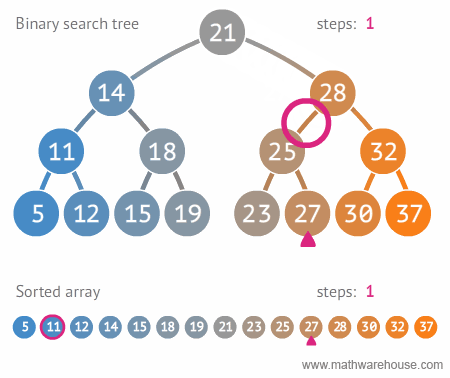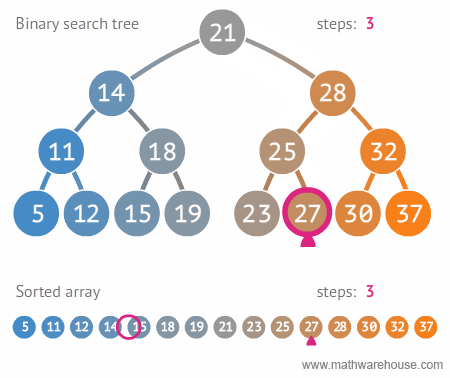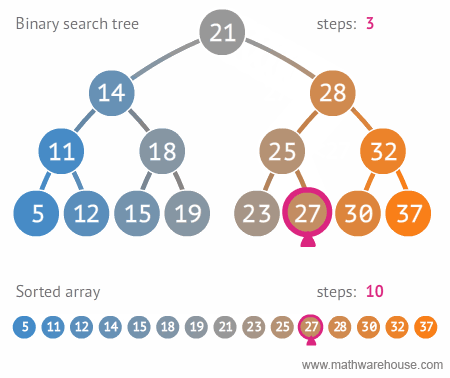
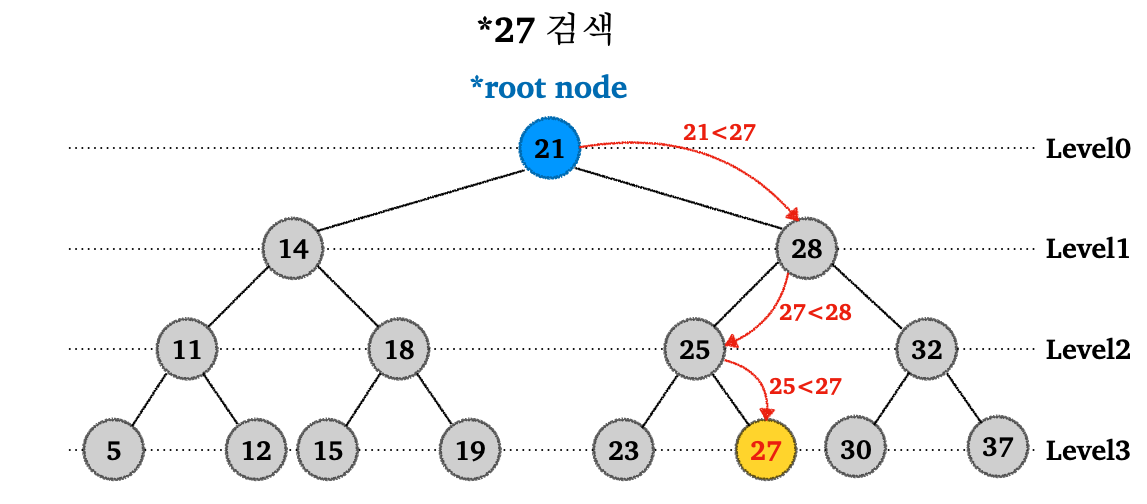
이번에는 이진 탐색 트리에서 특정 값을 검색하는 방법을 다음 그림을 통해 알아보자.

27이라는 값을 찾는다고 가정하자.

27을 루트 노드 21과 비교. 21 < 27 이므로 오른쪽 서브 트리 탐색
28 > 27 이므로 왼쪽 서브 트리 탐색
25 < 27이므로 오른쪽 서브 트리 탐색
27과 같기 때문에 27 찾기 완료!

애니메이션으로 살펴보자.

https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php

위 애니메이션에서도 확인할 수 있듯이 기존 정렬 배열에서는 11번의 연산이 필요한것과 달리, 이진 탐색 트리(BST)에서는 4번의 연산으로 찾을 수 있다.

이진 탐색 트리의 계산의 핵심은 단계별로 한쪽 서브트리를 탐색하지 않아도 되기 때문에 연산 횟수를 줄일 수 있다.

2.3 이진 탐색 트리의 성능

이진 탐색 트리의 검색/삽입/삭제의 평균 성능은 O(logn)이다. 검색 과정에서 탐색할 노드의 수가 줄어드는 과정을 숫자로 표현해보자.

총 64개의 데이터가 있다고 가정하자.

64 → 32 → 16 → 8 → 4 → 2 → 1 : 트리를 절반씩 날려가며, 총 6번의 연산으로 최종 노드 도달 가능
이것을 $log_2(n)$으로 표현할 수 있다

이렇기 때문에 이진 탐색 트리의 주요 작업의 평균 성능은 O(logn)으로 표현할 수 있다. 그러나 최악의 경우 이진 탐색 트리의 성능은 어떨까?

이진 탐색 트리의 성능이 최악인 경우는, 데이터가 계속 한쪽으로 치우쳐져서 마치 연결 리스트와 같은 구조를 가질 때 나타난다.

다음 애니메이션으로 살펴보자.

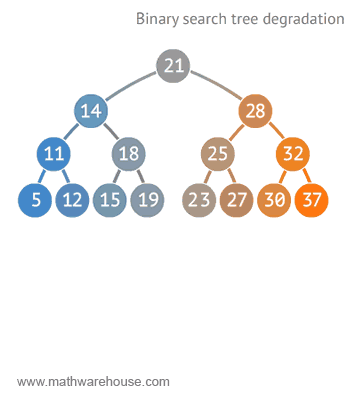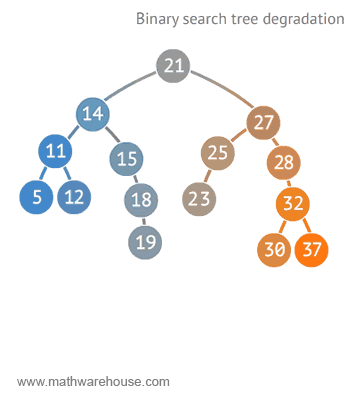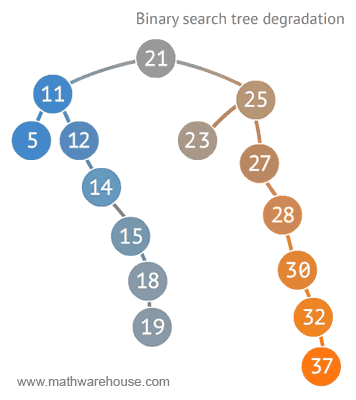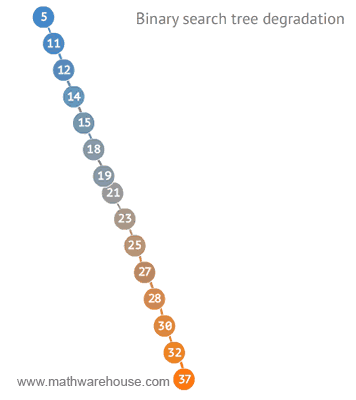https://www.mathwarehouse.com/programming/gifs/binary-search-tree.php

위의 경우 처럼 마치 배열 처럼 한줄을 이루게 되면, 성능은 최악의 경우 O(n)을 가지게 된다.

이런 문제를 해결하기 위해서 AVL 트리, Red-Black 트리와 같은 균형 이진 탐색 트리(Balanced Binary Search Tree)가 등장한다. 실제로 자바 TreeSet 컬렉션은 Red-Black 트리로 구현되어 있다.

2.4 이진 탐색 트리 순회

이진 탐색 트리의 핵심은 데이터의 값을 기준으로 정렬해서 보관한다는 점이다. 이 때문에 정렬된 순서로 트리를 순회할 수 있다.

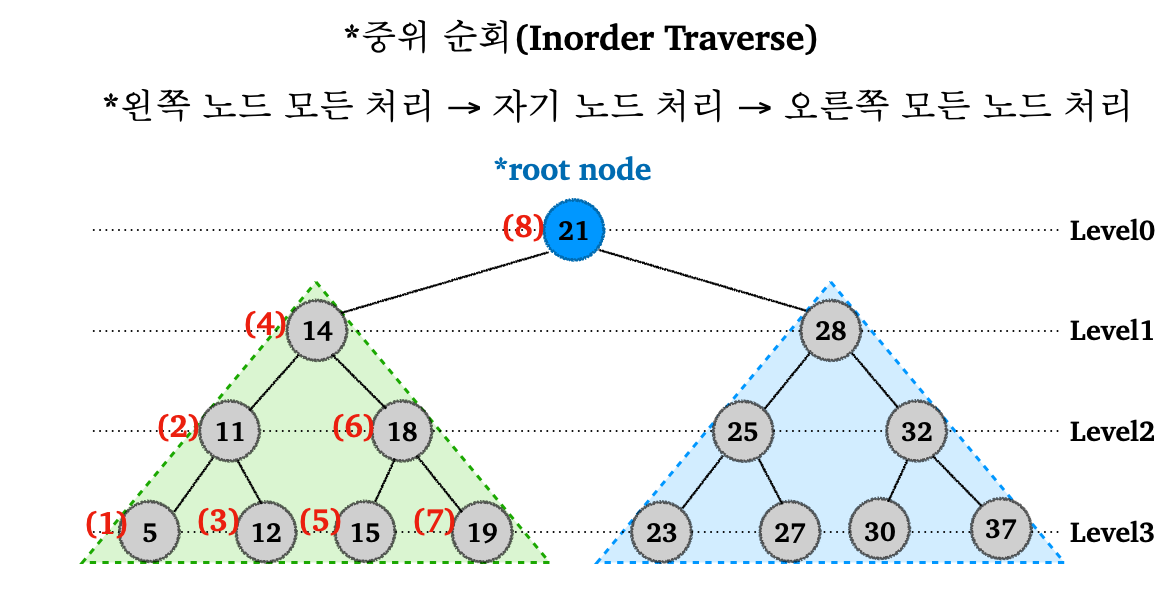
이진 탐색 트리의 경우 중위 순회(Inorder Traverse)를 사용한다. 이진 탐색 트리 특성상 노드를 오름차순으로 순회할 수 있다.

그림으로 살펴보자.

루트 노드 21을 기준 왼쪽 서브트리 방문
- 14 기준으로 왼쪽 서브트리 방문
  - 11 기준으로 왼쪽 서브트리 방문
    - 5 출력
  - 11 출력
  - 11 기준으로 오른쪽 서브트리 방문
    - 12 출력
- 14 출력
- 14 기준으로 오른쪽 서브트리 방문
  - 18 기준으로 왼쪽 서브트리 방문
    - 15 출력
  - 18 출력
  - 18 기준으로 오른쪽 서브트리 방문
    - 19 출력
21 출력
21 기준으로 오른쪽 서브트리 방문
이하 반복

Reference

1. 컴퓨터 공학(CS), 자료구조

data structure